CEA

Méthodes numériques de précision élevée et raffinement de maillage adaptatif

Contexte

Le développement de capacité de simulation de phénomènes physiques impliquant l'interaction d'ondes de choc avec des bulles de gaz ou liquide demande la résolution d'équations aux dérivées partielles. Cette résolution peut être réalisée à l'aide de méthodes numériques de précision élevée supplées par des techniques de Raffinement de Maillage Adaptatif (AMR) dans un contexte de parallélisme léger ou massif. L'AMR fournit un cadre dans lequel le maillage est enrichi dans les zones d'intérêt (onde, interface entre matériaux, etc.). La méthode numérique sous-jacente doit assurer la pertinence physique (positivité des densités et énergies), être relativement insensible aux erreurs de calcul et capturer une solution d'autant plus précise que la taille des maille de calcul est petite.
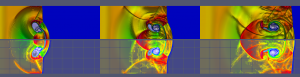
Ci-dessous l'interaction d'une onde de choc traversant le domaine de de gauche à droite et une bulle de gaz déformée en conséquence (couleur gris/bleu/blanc).

Références

1. M. Semplice, R. Loubère,
   Adaptive-Mesh-Refinement for hyperbolic systems of conservation laws based on a posteriori stabilized high order polynomial reconstructions.
   in revision J. Comput. Phys 2017.
2. M. Dumbser, R.Loubère,
   A simple robust and accurate a posteriori sub-cell finite volume limiter for the Discontinuous Galerkin method on unstructured meshes.
   Journal of Computational Physics,  Volume 319, 15, Pages 163–199, 2016.
3. R. Loubère and M. Dumbser and S. Diot,
   A New Family of High Order Unstructured MOOD and ADER Finite Volume Schemes for Multidimensional Systems of Hyperbolic Conservation Laws.
   Communication in Computational Physics, 16, pp. 718-763 (2014).

Contact

Raphaël LOUBERE : raphael.loubere@math.univ-toulouse.fr